优秀论文 | 成人的“数学模型”

成人的“数学模型”

你是一个零维的点，生活在一条一维的线上，你每天沿着这条线来回运动，你以为这就是世界的全部。直到有一天，在你前进的道路上出现了一个障碍（图1），它使得你无法继续前进。你以为这就是生命的尽头，于是你放下脚步，停止了追求。

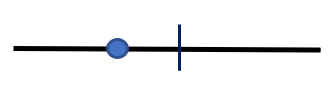
图1 一维空间生活示意图

突然有一天，你发现了二维空间。之前一维空间里无法克服的障碍，现在只需要借助于二维空间，从旁边绕过去即可（图2）。原来，世界还有这么多的未知空间等待我们去遨游。

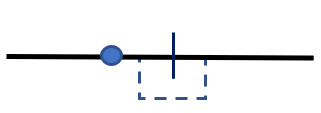
图2 二维空间生活示意图

可后来，你又一次遇到了困难。这次的困难与上次何曾相似，一条贯穿平面的线挡住了你的去路。你说，要在周围寻找可能翻越障碍的地方，可无论你如何左右奔波，都无法找到那个能让你翻越障碍的“捷径”。

直到有一天，你日日夜夜所生活的平面拔地而起，将你送向深远的高空，当你从高空俯视那条阻挡你前行的直线时，你才明白，那条看似不可跨越的线和当初阻挡你前行的点原来是一回事。三维空间的生活比起二维空间似乎要更加美妙——你不仅可以在平面上来回移动，甚至还可以将双脚解放，在天空中尽情翱翔。

你认为终于不会有东西来阻挡你。的确，短时间内还真不一定有这样的东西出现，但与此同时，其他的困难也在不断产生。

你发现，一维和二维空间里简单的生活一下子被打破：之前的一维空间里，大家都只有一条路可走，我们每个人的生活都有着丰富的交集。二维空间虽说有了很大的拓展，但每个人的轨迹还会多多少少有些交叉。但到了三维空间以后，我们发现我们很多时候都是在自己的轨迹上来回穿行，一位又一位曾经的朋友都在逐渐远离我们，尽管有时擦肩而过，道上几句亲切的问候，但要想完完全全地相交于一点，擦出独属于自己的亲密火花，困难还是很大。

本以为绚烂多彩的世界，一下子变得如此单调。虽说有了更多克服困难的方法，但这个单调的世界总让人觉得不是真实的世界，世界中的人不是真实的人，每个人都生活在虚拟之中，为了自己的利益而飞来飞去。每个人都总想要找到那个最遥远的地方，甚至有人为了找到人生的“极值点”而放弃了最基本的原则——一切都没有束缚，一切都充满了“自由”，“成人”的道路从未变得如此容易。

本以为空间维度的拓展会给大家的成人之路带来更多便利与自由，但最终所达到的效果却与我们最初的期待相差甚远，不被大家所期待的成人永远不是真正的成人。看来，要想为成人建立起一个恰当的数学模型，远远不是增加几个维度那么简单，那么，成人之路到底该如何走下去呢？

人之为人，从襁褓之中的婴儿，到耄耋之年的老人；不论是闻名于世的显赫之人，还是默默耕耘的普通人，都有着作为人的一系列基本特征：或如孔子所言之“仁性”，或如庄子所言之“天性”，又或如慧能所言之“悟性”。

多种性质构成了一个人区别于动物和其他人的最基本的几个特点。如果我们用x_1, x_{2, ...,} x_n来表示每个人的每一类特性，其中这些特性构成一个n元关系。如果我们用f来表示这样一个关系，那么，一个人的所有特征就可以用一个方程f（x₁, x₂, ..., x_n）=0来表示。由于每一个n元方程都可以在n维空间上表示一个确定的几何图形，因此从这个意义上来讲，我们之前所讨论的三维空间中每个人的个人轨迹都可以用一组方程来定性地表达。

现在，我们已经从最基本的人生轨迹出发，建立了对应的数学模型，那么下一步要做的就是要从数学模型出发，寻找成人的方法。

我们不妨先从最简单的方程——函数开始，展开我们的讨论。亚当·斯密在《国富论》中揭示了人类社会生产力发展的一般规律，指出了人类所有经济活动的最终目的，便是使得社会生产的效率达到最大化，从而创造出更多的社会财富。出于人类这样一种在自利心驱使下的对于财富追求的天然理性，对于人生而言，如果想要实现其价值，那么在大多数情况下，最终要达到的结果亦是使得某个要素得到最大化。

这样一个实际问题反映到n元函数上，便是要求得该函数的极值。要找到极值点，首先要找到使得该n元函数的偏导数等于零的点M（m₁, m₂, …, m_n）。然而，大多数情况下，偏导数为0并不意味着极值点的存在，而且一个函数的极值点也并不会只有一个。那么到底哪个才是我们追求的真正的“最值点”呢？

一个一个去尝试是一种方法，但这种既毫无头绪又占用时间的方法在生命有限的情况下完全不具有可操作性。而且，从孟德斯鸠的自由理论出发，一切的自由都需要在一个有法可依的基本社会框架下实现。换言之，每一个函数都拥有其唯一确定的“定义域”，它规定了这个函数有现实意义的范围，离开了这个范围所得到的任何结果，都不能成为指导实践的依据。有些通向无穷的间断点尽管可以得到一个很好的结果，可一经尝试，我们便会违反最基本的社会规定，陷入“死胡同”，再也无法走出来，一生也就这样草草结束了。

从另一个角度来看，你可以追求人生轨迹函数的极值点，别人同样可以追求人生轨迹函数的极值点。假如大家都去追求极值点，从理论上来讲行得通，可是从《国富论》看来，一切经济活动都是建立在大量的相关经济活动的基础之上的，即使是最简单的一把剪刀的制作，背后都需要成千上万份的其他类型劳动作为支持。因此，一旦一个人未能按照事先确定的轨迹行进，而是盲目去追求极值，势必会给其他人带来一定的影响。

那么我们该如何权衡自我成人与他人成人之间的关系，进行后续的选择呢？

既然为人，那么就完全脱离不了社会，你可以有一个人生轨迹，别人也可以有。现假设另有n人，其人生轨迹分别用f₁, f₂, …, f_n来表示，多条轨迹构成了n个各具特征的几何图形，从而大大增加了空间的丰富性。空间中元素的增多意味着复杂性的增加，同样也意味着更多复杂关系的出现。当空间中只存在一个几何体时，再怎么进行深入的讨论，也无法展现空间中多元关系的丰富性。可是，一旦空间中的元素多了起来，也便会有越来越多的新关系被引入。

在这里，我们选择另外一种函数的表示方法——选取其中一个变元x_i，利用泰勒公式将每个函数展开为无限个多项式的和，也就是幂级数。这样，不同的函数就可以由一组基本多项式（1, x_i¹, x_i², ..., x_i^m, x₁, x₂, ..., x_n）通过不同的线性组合表示，也就更有利于我们发现不同函数之间的关联，进而找到人与人之间更深层次的关联。

什么样的人是更加完美的？如果从构成的基本多项式上来讲，种类越多，线性关系越复杂，相对来讲就容易具有更多的性质，于人而言，便是“博雅”。“博者大通”，如果你展开后仅仅只是一个常数c，这样的生命毫无意义可言，一生所做只不过是“守株待兔”，期待可能出现的“交点”，也就是可能得到的机遇。而且，由于你可以调用的资源极其有限，所能够表达出的函数方程类型将始终停留在相对简单和固定的状态。比如，缺少了x²项，就无法表达e^x。

尽管有时可以通过更为复杂的线性组合表达出同样的结果，但这会使得表达形式变得极其复杂，可操作性也会大大降低。因此，一旦遇到困难，也就很难使目前稍有些偏差的人生轨迹得以修正，其结果也只能是一直这样偏着走下去，离最初所规划的人生目标越来越远。“雅者典正”，如果线性组合的方式与大多数人存在较大的偏差，那么这样的道路终究也只能有很小的机会得到与社会的交汇点。

而随着基本多项式的扩充和线性组合方式的完善，我们也便更能够演绎出适合于我们自身的人生轨迹，得到更多与社会中其他人的交点，进而在掌握自己人生发展方向的同时，为他人的成人和社会的良序发展发挥自己不可或缺的作用。

现在看来，成人的数学模型已经比较完善了，但如果按照这个模型深入探究下去，我们会发现一些十分荒唐的现象。比如，当我们任取两个方程和联立时，最终求出的解可能会有很多种，而每一个解都唯一对应一种人生状态。

拿《红楼梦》举例，我们设方程组的解为y，当y=y₁时，意味着宝黛初相见，当y=y₂时，意味着后续爱情故事中的某一段对话，如此推演下去，当y=y_n，也便是走过最后一组解时，两人从此以后再无交集，爱情故事也就到此终了。

有人说，既然最后终究摆脱不了分别的悲剧，那又为何要在现在如此倾心呢？是啊，我们人生中有太多最终必然会失去的东西，可我们为何要如此倾注于此呢？

其实，我们都忽略了一点，我们都固执地认为人生是唯一确定不变的：人生的一切都由我们为人的一些最基本的特性来确定，每一部分的特性作为整个n维空间的一个基底，通过适当的线性组合去构建一个向量场，从而表达我们从出生到死亡的完整人生轨迹。

然而，我们不难发现，这样一个模型实际上存在着许多问题。一方面，假如我们的人生从一开始就唯一确定了，那么我们为何还要努力奋斗呢？如果牛顿在出生之时就知道自己会提出牛顿运动定律，为什么还要去努力学习呢？退一步来讲，如果我们知道了我们会在十年后的某个时间死亡，那么我现在就自杀，是不是这个模型就错了呢？

另一方面，当我们一旦遇到某些不顺利的地方，我们通常会选择在目前模型上增加一个干扰项x₀，进而实现更加稳定的表达。就如同我们在一开始提到的那个问题，当我们在一维的线上遇到障碍物时，我们选择从二维空间绕行，当我们在二维的面上遇到障碍物时，我们选择从三维空间绕行，每当我们在现在的n维空间中无法得到解决方案时，我们就到n+1维空间中去寻求解决方案。虽然说这种方法更加简便，然而大量实验事实却证明，这种方法在增加数量较少的干扰项时，根本无法满足优化模型的目的。换言之，我们需要增加非常多的干扰项才能最终解决模型的优化问题。

但干扰项的增加总还是有一个限度的，随着空间的维数的增加，算法的复杂度也会成倍地增加，这种以时间换空间的解决方案远远超过目前人类所能实现的计算能力。可见，这样一个模型从最开始的设计上就存在着很多问题，那么问题出在了哪呢？

综合来看，以上所有的分析把矛头都指向了我们无时无刻不在经历的东西——时间。时间是一个神奇的事物，许多科学家都曾指出，时间不是绝对的旁观者，它和我们这个世界上的每一件事物一样，都是我们这个丰富多彩的世界中的一部分。不仅我们的一举一动和时间有着密切的联系，时间也在受到我们的控制。我们之前所确定的每一个函数关系，实际上都受到时间t的影响，即f（x₁, x₂, …, x_n, t）=0，同样地，每一个人生要素x₁, x₂, …, x_n也都受到时间t的影响，即它们也都是时间t的函数——x₁=x₁(t), x₂=x₂(t),…, x_n=x_n(t)。

我们之前所确定的那些变元，只不过是t=t₀时，向量α=(x₁, x₂, …,x_n)的一组特值。每一次与其他人的相遇都可以看作是对于这一组值的改写，每一次对于这一组值的改写同样都使得我们的人生轨迹方程发生一些改变，进而通过一次次的修正得到一个较为完善的人生轨迹方程。

尽管最后得到的结果可能仍不如意，但这样一种思路却为我们解决成人道路上的问题提供了新的方法。人生永远不再只是追求唯一最优解的单调生活，每一个状态都可能会随着时间的变化由最优解变为非最优解，我们只需要根据目前的情况分析，找到能够使目前和一个可预知范围内的效益最大化的解，从而描绘出人生的轨迹方程。

因此，对于在n维空间中遇到的每一个障碍物，我们都可以选择等待时间带来改变，等到那个障碍物不再出现的时候，跨过它，得到人生的“新解”。

现在，我们回顾以上所有的推导过程，相信每一个认真看的人都会发现一个问题——既然每一个要素都是和时间有关的，那么时间呢？如果时间是唯一确定的话，我们不还是能够通过时间的方程来推演出后续结果吗？

的确，这样一种可能性是存在的，而且，按照这个思路出发，我们会发现这样的推理总会找到新的变元，如此循环下去，我们的函数关系就变成了lim_n→∞f(x₁, x₂, ..., x_n, t₁, t₂, ..., t_n)=0，显然，这样一个方程显然非常复杂，当然也从一个侧面反映出建立一个完美的“成人”模型的难度很大。

对于这样一个无限递归的问题，著名的逻辑学家哥德尔曾得到一个著名结论，即“哥德尔不完全性定理”，它系统地阐述了一个系统内部逻辑推理系统的问题，指明了在这样一个系统中总存在一些仅仅依靠系统中所允许的方法既不能证实也不能证伪的命题。我们的模型也是如此，只要愿意去寻找，我们总能找到一些模型本身所存在的漏洞，发现一些成人的过程中仅凭借已知的知识无法解决的问题。正如苏轼在《题西林壁》中所言“不识庐山真面目，只缘身在此山中”。

成人如登山，我们渴望看遍山花烂漫，解密山林深处的每一处细节，遇见每一个我们想要遇见的人，从而确定我们要留下的每一个脚印的位置。

按照与上述分析相反的过程，我们可以将这样一条道路用有限个变元所确定的一个方程表示出来，进而得到我们关于这座山的一份完整的认识。可直到我们从山中走出，以一个山外人的角色来看待我们自以为详细地了解过的这座山时，我们才会明白，原来，山是如此简单。

但是，这丝毫不影响我们对于山的探索。我们依旧在积极去遇见人生中的偶然，去延拓已知人生的宽度，去解构人生的基本元素，去发现人生的基本规律，每一步都带着探索的精神，去完善我们前一步所确定的模型，即目前的方程f_n=g_{n °} f_n-1。

这样，我们所迈出的每一步都是我们目前最好的选择，经过每一步的体验后所修正的模型都是目前最好的模型，而这些一小步累积起来的道路，也便是我们成人的道路，经过了每一次修正所得到的方程结合起来，也便是那个唯一确定的最优的成人轨迹方程。